Patnácka
Do dnešních časů přežila krabička s šestnácti políčky a patnácti očíslovanými kameny, o níž matematik Ahrens napsal: "Hra v patnáct se rychle rozšířila ze Spojených států a pro obrovský počet vášnivých hráčů, kteří jí propadli, se proměnila ve skutečné společenské zlo."
Cílem hry je seřadit přeházené kameny posunem vodorovně nebo svisle do správného pořadí podle obr. 1. Na začátku se kameny vysypaly a buď náhodně uložily do krabičky, nebo se zadávaly úlohy. Na jejich řešení byly v hráčských klubech vypisovány vysoké odměny. Tu nejznamenitější úlohu vymyslel právě Sam Loyd. Na její řešení vypsal tisíc dolarů, což byly v sedmdesátých letech minulého století velké peníze. Tak vznikla ta obrovská honička za odměnou. Peníze však nebyly nikdy vyplaceny, nikdo nedokázal přesunout kameny ze zadaného postavení (obr. 2) do základního postavení (obr. 1).
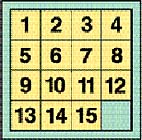
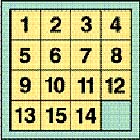Již jsme si řekli, že Samuel měl skvělou hlavu. A taky chytrou. Nic neriskoval. Jak dokázali později matematikové, úloha neměla řešení! Z mnoha možných náhodných postavení je polovina neřešitelných. Abychom vám ušetřili trápení s řešením nemožných úloh, prozradíme vám tajný systém, podle kterého již na počátku dokážete rozlišit řešitelnou úlohu od neřešitelné. Je-li v pořadí kamenů vyšší kámen před nižším, je to tzv. inverze (např. 5 před 4). Spočítáme všechny inverze, které v postavení jsou. Sudý počet inverzí znamená, že úloha je řešitelná. Lichý počet inverzí je v neřešitelných úlohách. Ve zmiňované Loydově úloze je jediná inverze, tedy lichý počet, a proto je neřešitelná.
Doufáme, že znalosti tajného systému nevyužijete k uzavírání předem vyhraných sázek na řešení neřešitelného. A dělat naivního: "Hele, já s tím nemohu hnout, o dvacku, že to taky nevyřešíš!"
