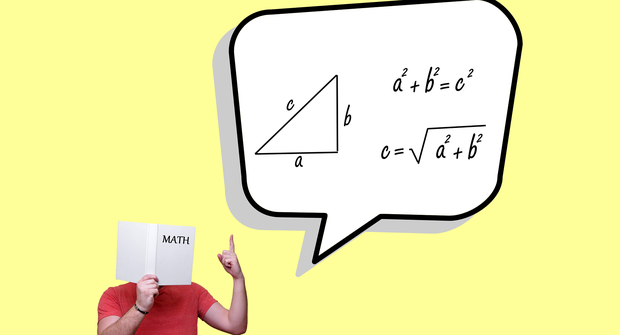Australský matematik Daniel Mansfield z univerzity v Sydney propojil jeden z nejpropracovanějších matematických objektů starověku Plimpton 322 s problémem znázorněným na ještě starší hliněné destičce s označením Si.427, kterou objevil v istanbulském muzeu.
Plimpton 322
Dosud se totiž mělo za to, že jedním z nejpozoruhodnějších a nejstarších matematických objevů ze starověku je objekt známý jako Plimpton 322. Jde o fragment hliněné tabulky ze starověké Mezopotámie. Archeolog, dobrodruh, akademik a prodejce starožitností Edgar Banks jej prodal asi v roce 1922 slavnému vydavateli a sběrateli George Plimptonovi, který jej poté spolu se zbytkem své sbírky odkázal v roce 1936 Kolumbijské univerzitě.
Pythagorova věta
Plimpton 322 obsahuje tabulku diagonálních tzv. „pythagorejských trojic“. Pythagorejská trojice je v matematice trojice přirozených čísel a, b, c (tj. celých kladných čísel), které lze využít jako velikosti stran pravoúhlého trojúhelníka. Následně se stal Plimpton 322 jedním z nejzajímavějších a nejvíce studovaných matematických objektů starověkého světa. K čemu všemu a kdy se trigonometrické znalosti využívaly, přinesla odpověď další hliněná a ještě starší deska Si.427.
Babyloňané a Si.427
Starověká hliněná deska, která nese označení Si.427, byla objevena a katalogizována spolu s mnoha dalšími deskami francouzskou archeologickou expedicí z roku 1894 v Sipparu ve středním Iráku. Si.427 pochází ze starého babylonského období (1900-1600 př. n. l.) a je jediným známým příkladem katastrálního dokumentu z tohoto období, který používají geodeti pro určení hranice pozemků.
Jak rozdělit pole?
Tato konkrétní destička udává právní a geometrické detaily o poli, které bylo rozděleno poté, co byla jedna jeho část prodána. Zeměměřič na ní používá k určení přesných pravých úhlů Pythagorovu větu, která ovšem byla definována až o tisíc let později! Pythagorova věta popisuje vztah, který platí mezi délkami stran pravoúhlých trojúhelníků v rovině. Umožňuje dopočítat délku třetí strany takového trojúhelníka, pokud jsou známy délky dvou zbývajících stran. Dosud vědci netušili, že Babyloňané využívali trigonometrii pro řešení praktických problémů své doby.
Chytří geodeti
Stejně jako další dochované plány si Si.427 zachovává rozdělení země na obdélníky, pravé lichoběžníky a pravé trojúhelníky. Ale na rozdíl od dřívějších terénních plánů se týká prodeje soukromých pozemků a měření byla provedena s neobvykle vysokou přesností. Samotné obdélníky jsou nejpozoruhodnější, protože ve skutečnosti mají protilehlé strany stejné délky, což je jedinečné a naznačuje, že starobabylonští geodeti vymysleli způsob, jak vytvořit kolmé čáry přesněji než dříve.
Udělat pravý úhel je věda
Vytvoření přesných kolmých čar je náročný úkol, který obvykle vyžaduje speciální vybavení. Jak to dokázat mohl zeměměřič pouhou měřicí tyčí, lanem a kolíčky? Odpověď leží na hranicích pozemků, kde najdeme tři tvary (dva obdélníky a pravý trojúhelník) s rozměry diagonálních trojic. Kolmé strany těchto tvarů byly pravděpodobně prodlouženy zrakem, aby vytvořily linie nalezené v dělení. Neobvyklé je také zvolení diagonálních trojic 5-12-13 a 8-15-17, místo obvyklé trojkombinace 3-4-5. Vědci se domnívají, že byly vybrány z toho důvodu, že je možné pro přepočet libovolně změnit měřítko.
Kde leží základ?
Staří Babyloňané byli schopní vytvořit přesné kolmé čáry z různých diagonálních trojic a zvláště užitečné byly ty s pravidelnými stranami. Jestli je možné, že se Plimpton 322 inspiroval právě touto katastrální hliněnou destičkou a kde vzal inspiraci sám slavný řecký filozof, matematik a astronom Pythagoras ze Samu, už se asi nedozvíme.